Задача
С помощью циркуля и линейки проведите через общую точку A окружностей S1 и S2 прямую так, чтобы эти окружности высекали на ней равные хорды.
Решение
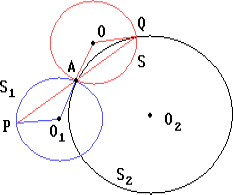
Предположим, что нужная прямая проведена. Пусть PA = QA — равные хорды окружностей S1 и S2, лежащие на этой прямой.
При симметрии относительно точки A точка P переходит в точку Q, а окружность S1 — в равную ей окружность S, проходящую через точку Q.
Отсюда вытекает следующий способ построения. Строим окружность S, симметричную данной окружности S1 относительно данной точки A. Точка пересечения окружностей S и S2, отличная от A, лежит на искомой прямой.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет