Задача
Точка M лежит на диаметре AB окружности. Хорда CD окружности проходит через точку M и пересекает прямую AB под углом в 45°.
Докажите, что величина CM² + DM² не зависит от выбора точки M.
Решение
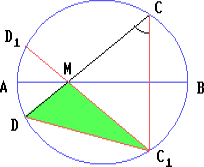
Пусть C1 – точка, симметричная точке C относительно прямой AB. Точка C1 лежит на данной окружности, так как сама окружность симметрична относительно диаметра AB. Поскольку ∠C1MD = 90°, то CM² + DM² = C1M² + DM² = C1D², а ∠C1CD = ∠AMD = 45°. Поэтому длина C1D, а значит, и сумма CM² + DM² не зависит от выбора точки M.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет