Задача
Окружность, построенная на высоте AD прямоугольного треугольника ABC как на диаметре, пересекает катет AB в точке K, а катет AC — в точке M. Отрезок KM пересекает высоту AD в точке L. Известно, что отрезки AK, AL и AM составляют геометрическую прогрессию (т.е. ${\frac{AK}{AL}}$ = ${\frac{AL}{AM}}$). Найдите острые углы треугольника ABC.
Решение
Поскольку AD и KM — диаметры указанной окружности, то четырёхугольник AKDM — прямоугольник. Пусть P — проекция вершины A на диаметр KM. Тогда
AL2 = AK . AM = KM . AP = AD . AP = 2AL . AP.
Отсюда находим, чтоAL= 2AP. Следовательно, в прямоугольном
треугольникеAPLуголAPLравен30o, а т.к.$\angle$ALP= 2$\angle$LAM, то$\angle$LAM= 15o. Значит,
$\displaystyle \angle$ACB = 90o - $\displaystyle \angle$DAC = 90o - $\displaystyle \angle$LAM = 75o, $\displaystyle \angle$ABC = 90o - 75o = 15o.
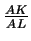
Ответ
15o, 75o.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет