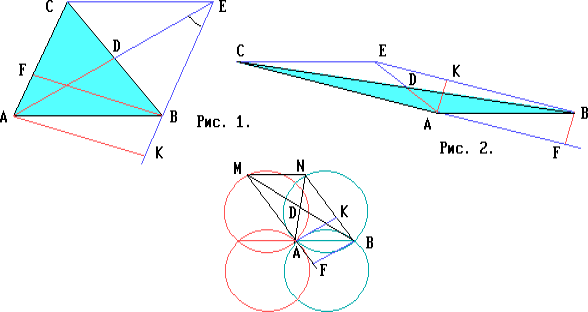
Пусть точка C удовлетворяет условию задачи, AD — медиана треугольника ABC, BF — высота, AD = BF. На продолжении отрезка AD за точку D отложим отрезок DE, равный AD. Тогда четырёхугольник ABEC — параллелограмм.

Предположим, что угол AEB острый. Пусть K — проекция точки A на прямую BE. Тогда

Поэтому$\angle$AEB= 30^o. Если уголAEBтупой, то аналогично получим, что$\angle$AEB= 150^o. Следовательно, все такие точкиEнаходятся на двух равных окружностяхS₁иS₂, которые общей хордойABделятся на дуги в300^oи60^o. Тогда все точкиCнаходятся на окружностяхS₁' иS₂', полученных изS₁иS₂параллельным переносом на вектор$\overrightarrow{BA}$. Докажем теперь, что любая точка M окружностей S₁' и S₂', кроме точек их пересечения, удовлетворяет условию.

Пусть M — произвольная точка одной из этих окружностей, отличная от их точки пересечения. При параллельном переносе на вектор $\overrightarrow{AB}$ точка M переходит в некоторую точку N одной из окружностей S₁ или S₂. Если AD — медиана треугольника ABM, BF — его высота, K — проекция точки A на прямую NB, а $\angle$ANB = 30^o, то

т.е. точкаMудовлетворяет условию. Аналогично для второго случая ($\angle$ANB= 150^o). Итак, все точки окружностей S₁' и S₂', кроме концов их общей хорды, удовлетворяют условию.

Две равные пересекающиеся окружности без точек их пересечения.