Задача
На сторонах остроугольного треугольника ABC взяты точки A1, B1, C1 так, что отрезки AA1, BB1, CC1 пересекаются в точке H.
Докажите, что AH·A1H = BH·B1H = CH·C1H тогда и только тогда, когда H – точка пересечения высот треугольника ABC.
Решение
Если H – точка пересечения высот треугольника ABC, то треугольники AHB1 и BHA1 подобны. Следовательно, AH : BH = B1H : A1H, или AH·A1H = BH·B1H.
Аналогично BH·B1H = CH·C1H. Пусть теперь AH·A1H = BH·B1H = CH·C1H.
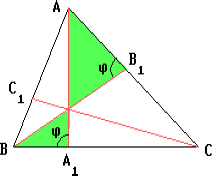
Тогда треугольники AHB1 и BHA1 подобны. Обозначим ∠AB1H = ∠BA1H = φ. Тогда ∠CA1H = ∠CB1H = 180° – φ.
Аналогично ∠BC1H = ∠CB1H = 180° – φ, ∠AC1H = ∠CA1H = 180° – φ. Следовательно, ∠AC1H = ∠BC1H = 90°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет