Задача
На стороне BC равностороннего треугольника ABC как на диаметре внешним образом построена полуокружность, на которой взяты точки K и L, делящие полуокружность на три равные дуги. Докажите, что прямые AK и AL делят отрезок BC на равные части.
Решение
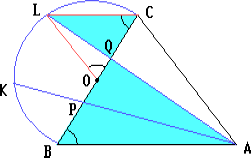
Пусть O – середина BC, P и Q – точки пересечения отрезков AK и AL со стороной BC.
Поскольку ∠LOC = 60° и OL = OC, то треугольник LOC – равносторонний. Поэтому LC = OC = ½ BC = ½ AB, LC || AB.
Из подобия треугольников LQC и AQB находим, что CQ = LC/AB·BQ = ½ BQ.
Следовательно, CQ = 1/3 BC. Аналогично BP = 1/3 BC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет