Задача
Три равных окружности S1, S2, S3попарно касаются друг друга, и вокруг них описана окружность S , которая касается всех трёх. Докажите, что для любой точки M окружности S касательная, проведённая из точки M к одной из трёх окружностей S1, S2, S3, равна сумме касательных, проведённых из точки M к двум другим окружностям.
Решение
Пусть O1, O2, O3, O — центры окружностей S1, S2, S3, S соответственно; A1, A2, A3— точки касания окружностей S1, S2, S3с окружностью S . Предположим, что точка M лежит на дуге A1A2, не содержащей точки A3. Обозначим через α , β , γ углы между лучом OM и лучами OO1, OO2, OO3соответственно. Тогда, если r — радус каждой из трёх меньших окружностей, а R — радиус большей, то по теореме косинусов
MO12 = R2 + (R-r)2 - 2R(R-r) cos α,
MO22 = R2 + (R-r)2 - 2R(R-r) cos β,
MO32 = R2 + (R-r)2 - 2R(R-r) cos γ.
MO12 - r2 = 2R(R-r)(1 - cos α) =
4R(R - r) sin 2 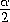 ,
,
MO22 - r2 = 2R(R-r)(1- cos β) =
4R(R-r) sin 2 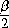 ,
,
MO32 - r2 = 2R(R - r)(1 - cos γ) =
4R(R - r) sin 2 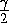 .
.
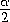 sin
sin 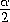 ,
2
,
2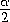 sin
sin 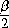 ,
2
,
2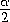 sin
sin 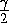
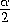
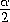
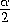 180o,
0
180o,
0 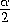
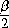
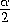 180o,
0
180o,
0 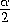
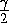
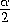 180o).
180o).
sin 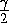 = sin
= sin 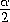 + sin
+ sin 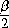 .
.
Действительно, рассмотрим равносторонний треугольник A1A2A2. Точка M лежит на его описанной окружности, поэтому MA1+MA2=MA3, а т.к.
MA1=2R sin 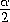 ,
MA2=2R sin
,
MA2=2R sin 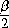 ,
MA1=2R sin
,
MA1=2R sin 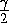 ,
,
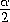 + 2R sin
+ 2R sin 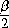 =
2R sin
=
2R sin 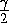 .
.
Следовательно,
sin 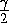 = sin
= sin 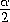 + sin
+ sin 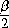 .
.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь