Пусть O, O₁, O₂ – данные центры в указанном порядке. Построим на отрезке O₁O₂ как на диаметре окружность. Тогда две вершины треугольника лежат на этой окружности, а её центр лежит на описанной окружности (см. задачу 156961 б) и на биссектрисе третьего угла.

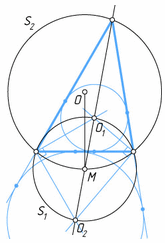
  Отсюда вытекает следующий способ построения. Строим на отрезке O₁O₂ как на диаметре окружность S₁. Пусть M – середина O₁O₂, то есть центр этой окружности. Радиусом OM строим окружность S₂ с центром O. Пересечение окружностей S₁ и S₂ даёт две вершины искомого треугольника, а пересечение прямой O₁O₂ с окружностью S₂ – третью вершину.

Ответ задачи отсутствует