Задача
Дана окружность, её диаметр AB и точка C на этом диаметре. Постройте на окружности две точки X и Y, симметричные относительно диаметра AB, для которых прямая YC перпендикулярна прямой XA.
Решение
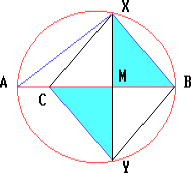
Предположим, что искомые точки X и Y построены. Тогда $\angle$AXB = 90o. Поэтому XB || YC.
Пусть M — точка пересечения отрезка XY с диаметром AB. Прямоугольные треугольники XMB и YMC равны (по катету и острому углу). Следовательно, CM = MB, т.е. M — середина отрезка BC.
Отсюда вытекает следующее построение. Через середину M отрезка BC проводим прямую, перпендикулярную данному диаметру AB. Эта прямая пересекает окружность в искомых точках X и Y.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет