Задача
На хорде AB окружности S с центром в точке O взята точка C. D — вторая точка пересечения окружности S с окружностью, описанной около треугольника ACO. Докажите, что CD = CB.
Решение
Рассмотрим случай, когда точки D и C лежат по разные стороны от AO. Пусть $\angle$DOC = $\alpha$. Тогда
$\displaystyle \angle$DAC = 180o - $\displaystyle \alpha$, $\displaystyle \angle$DOB = 360o - 2$\displaystyle \angle$DAB =
= 360o - (360o - 2$\displaystyle \alpha$) = 2$\displaystyle \alpha$.
Значит,OC— биссектриса углаDOB.
Поскольку треугольникDOBравнобедренный, то прямаяOC—
серединный перпендикуляр к отрезкуDB. Следовательно,CD=CB.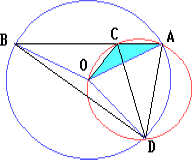
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет