Задача
Пятиугольник ABCDE вписан в окружность. Расстояния от точки A до прямых BC, CD и DE равны соответственно a, b и c.
Найдите расстояние от вершины A до прямой BE.
Решение
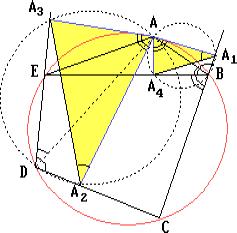
Пусть A1, A2, A3, A4 – основания перпендикуляров, опущенных из точки A на прямые BC, DC, DE и BE соответственно.
Точки A1 и A4 лежат на окружности с диаметром AB, а точки A1 и A1 – на окружности с диаметром AD. Поэтому ∠AA1A4 = ∠ABE = ∠ADE = ∠AA2A3,
∠A1AA4 = ∠CBE = ∠A2AA3.
Следовательно, треугольники AA1A4 и AA2A3 подобны и AA1 : AA2 = AA4 : AA3. Отсюда AA4 = AA1·AA3/AA2 = ac/b.
Ответ
ac/b.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет