Обозначим данные точки M₁, M₂, ..., M₁₉₈₃. Рассмотрим на окружности две произвольные диаметрально противоположные точки N₁ и N₂. Согласно неравенству треугольника, учитывая, что  N₁N₂ = 2,  для каждой точки M_i можно записать  M_iN₁ + M_iN₂ ≥ 2.  Сложив эти неравенства, получим 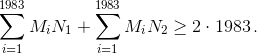    Значит, хотя бы одна из двух сумм в левой части последнего неравенства не меньше 1983.

Ответ задачи отсутствует