Олимпиадная задача по планиметрии для 8-9 класса: биссектриса в равностороннем треугольнике

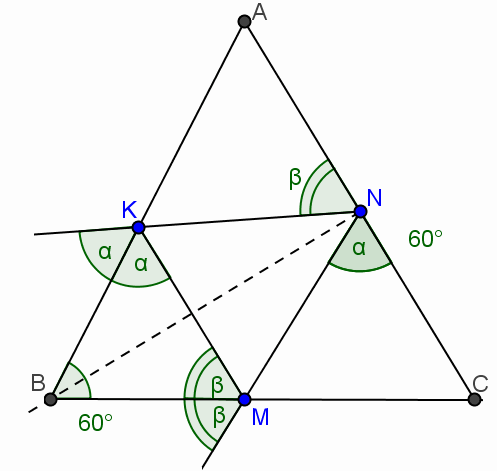
Пусть  ∠MKB = ∠MNC = α,  ∠KMB = ∠KNA = β  (см. рис.). Из треугольника KMB получим, что  α + β = 120°.  Теперь из треугольников NKA и NMC видно, что  ∠NKA = α,  ∠NMC = β.

Значит, и углы, вертикальные углам NKA и NMС, равны α и β соответственно. Следовательно, лучи KB и MB являются биссектрисами внешних углов треугольника KNM. Так как биссектрисы двух внешних углов треугольника и биссектриса внутреннего угла при третьей вершине пересекаются в одной точке, то NB – биссектриса угла MNK.

Ответ задачи отсутствует