Олимпиадная задача по планиметрии: диагонали и прямые углы в четырёхугольнике

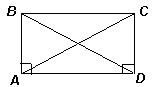
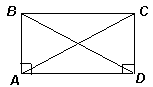
  Рассмотрим четырёхугольник ABCD, в котором  АС = BD.  Возможны два случая: прямые углы либо соседние, либо противоположные.

  1) Пусть углы A и D – прямые (рис. слева). Тогда прямоугольные треугольники ABD и DCA равны по гипотенузе и катету. Следовательно,  АВ = DC.  Кроме того,  АВ || DC. Таким образом, ABCD – параллелограмм с прямым углом, то есть – прямоугольник.

  2) Пусть углыAиС– прямые, тогда точкиAиCлежат на окружности с диаметромBD(рис. справа). Так как диаметр окружности является её наибольшей хордой, тоАС– также диаметр этой окружности; значит, углыВиD– также прямые.

Верно.