Олимпиадная задача по планиметрии для 8–10 классов от Кунгожина М.: угол между прямыми в треугольнике
Задача
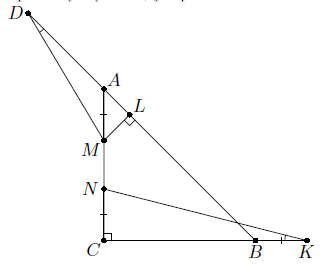
ABC – равнобедренный прямоугольный треугольник. На продолжении гипотенузы AB за точку A взята точка D так, что AB = 2AD. Точки M и N на стороне AC таковы, что AM = NC. На продолжении стороны CB за точку B взята такая точка K, что CN = BK. Найдите угол между прямыми NK и DM.
Решение
Пусть L – проекция M на AB. Заметим, что
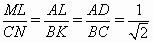; поэтому и 
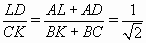. Значит, прямоугольные треугольники MLD и NCK подобны, и ∠MDL = ∠NKC (см. рис.). Поэтому угол между прямыми NK и MD равен углу между прямыми KC и LD, то есть 45°.
Ответ
45°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет