Как восстановить треугольник через циркуль и линейку — олимпиадная задача по планиметрии
Задача
В треугольнике ABC провели биссектрисы BB' и CC', а затем стёрли весь рисунок, кроме точек A, B' и C'.
Восстановите треугольник ABC при помощи циркуля и линейки.
Решение
Решение 1: Пусть I – центр вписанной окружности треугольника ABC, а O – центр описанной окружности Ω треугольника B'IC'. Как известно,
∠B'IC' = 90° + ½ ∠A (см. задачу 155448). Значит, ∠B'OC' = 180° – ∠B'AC'.
Таким образом, можно построить точку O, а затем – точку I (как точку пересечения меньшей дуги B'C' окружности Ω с биссектрисой угла B'AC', см. рис.). Теперь точки B и C строятся как пересечение прямых B'I, AC' и C'I, AB' соответственно.
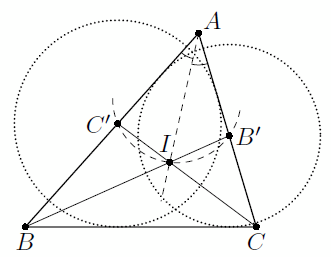
Решение 2: Точка B' равноудалена от прямых BC и AB. Поэтому окружность с центром B', касающаяся AC', касается также BC. Аналогично прямая BC касается окружности с центром C', касающейся AB' (см. рис.). Следовательно, для восстановления точек B и C достаточно провести общую внешнюю касательную к этим двум окружностям (лежащую по другую сторону от B'C', чем A) и найти точки её пересечения с AB' и AC'.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь