Олимпиадная задача по планиметрии: высота, медиана и биссектриса в треугольнике

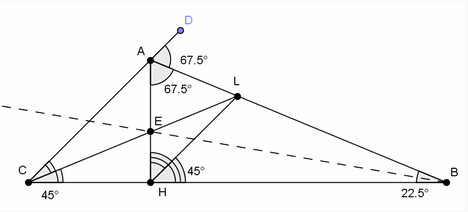
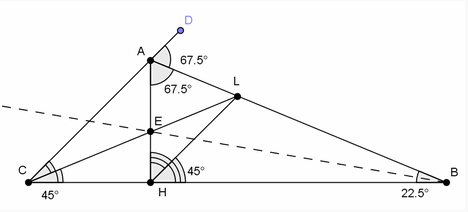
  Докажем сначала, что  AC || LH.   Первый способ. Пусть DАB – внешний угол данного треугольника. Он равен 67,5° (см. рис.).

  Из прямоугольного треугольникаABH:  ∠HАB= 67,5°.  Следовательно, в точкеLпересекаются внутренняя и внешняя биссектрисы треугольникаACH. ТогдаHL– еще одна внешняя биссектриса треугольникаACH, значит,  ∠LHB= 45° = ∠ACB.  Следовательно,  AC || LH   Второй способ. Заметим, что треугольник AHC – прямоугольный и равнобедренный (см. рис.).   Так как  ∠LCB= 22,5°,  то  ∠ALC= 45°  (внешний угол треугольникаBLC). Таким образом, точкаLлежит на окружности с центром в точкеHи радиусомHA. Значит,  ∠LHA= 2 ∠LCA= 45° = ∠СAН,  поэтому  LH || AC.   Итак, ACHL – трапеция, а отрезки CL и AH – ее диагонали. Пусть эти диагонали пересекаются в точке E. Так как В – точка пересечения продолжений боковых сторон трапеции, то прямая BE проходит через середину основания АС, то есть содержит медиану BM треугольника ABC (см. задачу 153749).

Ответ задачи отсутствует