Наибольшая степень двойки, делящая 10^20 – 2^20: олимпиадная задача по математике

  10²⁰ – 2²⁰ = 2²⁰·5²⁰ – 2²⁰ = 2²⁰·(5²⁰ – 1). Далее можно рассуждать по-разному.   Первый способ. 5²⁰ – 1 = (5¹⁰ – 1)(5¹⁰ + 1) = (5⁵ – 1)(5⁵ + 1)(25⁵ + 1) =

     = (5 – 1)(5⁴ + 5³ + 5² + 5 + 1)(5 + 1)(5⁴ – 5³ + 5² – 5 + 1)(25 + 1)(25⁴ – 25³ + 25² – 25 + 1) =

     = 2⁴·(5⁴ + 5³ + 5² + 5 + 1)·3·(5⁴ – 5³ + 5² – 5 + 1)·13·(25⁴ – 25³ + 25² – 25 + 1).

  Последние пять множителей – нечётные.   Второй способ.  5²⁰ – 1 = (1 + 4)²⁰ – 1 = 1 + 20·4 + 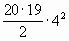+ ...+ 4²⁰ – 1 = 5·2⁴ + 10·19·2⁴ + ... + 4²⁰.

  В полученной сумме первое слагаемое делится только на 2⁴, а каждое из остальных – хотя бы на 2⁵. Значит, число  5²⁰ – 1  делится на 2⁴, но не на 2⁵.

На 2²⁴.