Олимпиадная задача по планиметрии для 8–9 классов: доказательство для треугольника АВС
Задача
Точка K – середина гипотенузы АВ прямоугольного треугольника АВС. На катетах АС и ВС выбраны точки М и N соответственно так, что угол МKN – прямой. Докажите, что из отрезков АМ, ВN и MN можно составить прямоугольный треугольник.
Решение
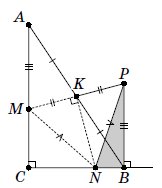
Решение 1:Продлим отрезок МK за точку K на его длину и получим точку Р (рис. слева). Из равенства треугольников BKP и АМK получим, что BР = AM и
BР || AM (а значит, BP ⊥ BN). В треугольнике MPN отрезок NK является высотой и медианой, следовательно, этот треугольник – равнобедренный: NP = MN. Таким образом, прямоугольный треугольник NBР – искомый.
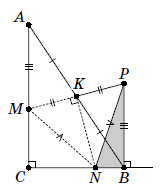
Решение 2:Дополнив все точки и отрезки, указанные в условии, им симметричными относительно точки K (рис. справа), мы получим прямоугольник ACBD и параллелограмм MNPQ. Так как угол MKN – прямой, то MNPQ – ромб, значит QM = MN. Из симметрии AQ = BN, и треугольник AQM – искомый.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь