Назад

Олимпиадная задача по планиметрии: круг в трапеции и равенство отрезков TB и TC

Задача 216851 • Сложность: 2 • 8-9 класс
Задача

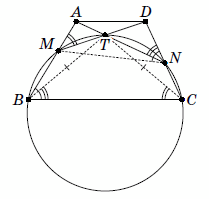
Через концы основания BC трапеции ABCD провели окружность, которая пересекла боковые стороны AB и CD в точках M и N соответственно. Известно, что точка T пересечения отрезков AN и DM также лежит на этой окружности. Докажите, что  TB = TC.

Разделы:
Планиметрия
Источники:
Окружная олимпиада (Москва) Олимпиады и турниры 2012 год 9 класс
Количество версий:
5
Решение

Так как четырёхугольник MBCN – вписанный, то  ∠MBC = ∠MND  (см. рис.).

Следовательно,  ∠MND+ ∠MAD= ∠MBC+ ∠MAD= 180°,  поэтому четырёхугольникMADN– также вписанный, и  ∠TCB= ∠TND= ∠TMA= ∠TBC.  Значит,  TB = TC.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет