Олимпиадная задача по планиметрии: отношение отрезков в параллелограмме (8-9 класс)
Задача
В параллелограмме ABCD диагональ АС в два раза больше стороны АВ. На стороне BC выбрана точка K так, что ∠KDB = ∠BDA.
Найдите отношение BK : KC.
Решение
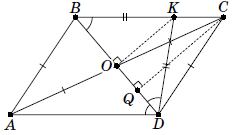
Пусть O – точка пересечения диагоналей параллелограмма. Из условия следует, что AB = AO = OC = CD (см. рис.).
Ответ
2 : 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет