Олимпиадная задача по стереометрии: покрытие основания пирамиды треугольниками, 10–11 класс

Решение 1:   Рассмотрим произвольную точку P основания и докажем, что она покрыта одним из треугольников. Возьмём маленькую сферу, лежащую внутри пирамиды и касающуюся основания в точке P (такая, очевидно, найдётся). Начнём увеличивать её радиус, сохраняя условие касания; тогда в некоторый момент она впервые коснётся боковой поверхности пирамиды. Пусть, скажем, она коснулась грани SA₁A₂ в точке Q (см. рис.).

  Тогда  PA₁=QA₁, PA₂=QA₂;  стало быть, треугольникиPA₁A₂иQA₁A₂равны. Это значит, что при повороте граниSA₁A₂вокругA₁A₂, переводящем её вX₁A₁A₂, точкаQпереходит вP, то естьPлежит внутриX₁A₁A₂.

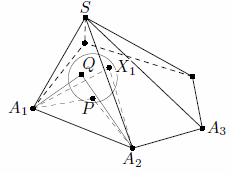
Решение 2:   Предположим, что некоторая точка P основания не покрыта треугольниками. Тогда для каждого i либо

∠PA_iA_i+1 > ∠X_iA_iA_i+1,  либо  ∠PA_i+1A_i > ∠X_iA_i+1A_i.  Без ограничения общности можно считать, что  ∠PA₂A₁ > ∠X₁A₂A₁.

  Если α, β, γ – плоские углы трёхгранного угла, то  α < β + γ;  поэтому  ∠A₁A₂A₃ < ∠SA₂A₁ + ∠SA₂A₃ = ∠X₁A₂A₁ + ∠X₂A₂A₃ < ∠PA₂A₁ + ∠X₂A₂A₃.  Значит,  ∠PA₂A₃ = ∠A₁A₂A₃ – ∠PA₂A₁ < ∠X₂A₂A₃.  Следовательно,  ∠PA₃A₂ >  ∠X₂A₃A₂.  Продолжая такие рассуждения дальше, получаем, что при любом  i= 1, 2, ...,n  верны неравенства  ∠PA_iA_i+1< ∠X_iA_iA_i+1  и  ∠PA_i+1A_i> ∠X_iA_i+1A_i.  Это значит, что отрезкиX_iA_i+1иPA_iпересекаются (см. рис.).

  Поэтому (см. задачу155162)  X_iA_i + PA_i+1<XA_i+1+PA_i,  то есть  SA_i+PA_i+1<SA_i+1+PA_i.  Но, складывая все такие неравенства, получаем (SA₁+ ... +SA_n) + (PA₁+ ... +PA_n) < (SA₁+ ... +SA_n) + (PA₁+ ... +PA_n).  Противоречие.

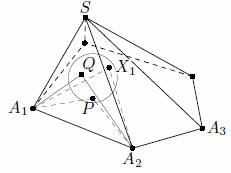
Ответ задачи отсутствует