Олимпиадная задача Агахановa: доказательство для многочленов и неравенств (9-10 класс)
Задача
Положительные действительные числа a1, ..., an и k таковы, что a1 + ... + an = 3k,
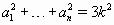и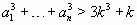 
.
Докажите, что какие-то два из чисел a1, ..., an отличаются больше чем на 1.
Решение
По условию
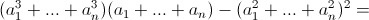
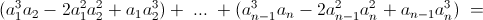
= a1a²(a1 – a2)² + ... + an–1an(an–1 – an)² > 9k4 + 3k² – 9k4 = 3k².
Если все разности наших чисел не больше 1, то
a1a2 + a1a3 + ... + an–1an > 3k². Но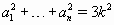 
Противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет