Олимпиадная задача по стереометрии: сумма длин отрезков между точками на гранях куба, 10–11 класс
Задача
Внутри каждой грани единичного куба выбрали по точке. Затем каждые две точки, лежащие на соседних гранях, соединили отрезком.
Докажите, что сумма длин этих отрезков не меньше, чем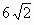 
.
Решение
Спроектируем четыре отрезка, соединяющие точки, лежащие на боковых гранях, на нижнюю грань куба. При этом длины отрезков не увеличатся. Мы получили четырёхугольник, вписанный в единичный квадрат. Докажем, что его периметр не меньше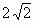 
. Аналогично оцениваются суммы длин ещё двух четвёрок отрезков.
Проекция отрезка отсекает от квадрата прямоугольный треугольник и служит его гипотенузой. Из неравенства 2(a2 + b2) ≥ (a + b)2 следует, что длина гипотенузы не меньше полусуммы катетов, умноженной на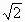 
. Поэтому сумма длин четырёх этих проекций не меньше полупериметра грани, умноженного на
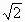, то есть не меньше .
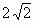Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь