Назад

Олимпиадная задача по комбинаторике: мини-слон и шахматная доска 5×5 для 7–9 классов

Задача 216671 • Сложность: 3 • 7-9 класс
Задача

Клетки доски размером 5×5 раскрашены в шахматном порядке (угловые клетки – чёрные). По чёрным клеткам этой доски двигается фигура – мини-слон, оставляя след на каждой клетке, где он побывал, и больше в эту клетку не возвращаясь. Мини-слон может ходить либо в свободные от следов соседние (по диагонали) клетки, либо прыгать (также по диагонали) через одну клетку, в которой оставлен след, на свободную клетку за ней. Какое наибольшее количество клеток сможет посетить мини-слон?

Решение

  Приведём вначале пример маршрута мини-слона, который обеспечит посещение им двенадцати клеток (см. рис., числа от 1 до 12 показывают порядок обхода клеток).

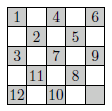
  Докажем, что все чёрные клетки мини-слон обойти не сможет. Рассмотрим четыре угловые клетки. Выйти из такой клетки мини-слон может либо в соседнюю клетку, либо в центральную. В соседнюю клетку из угловой он может пойти только первым ходом. Действительно, попасть в угловую клетку можно либо из соседней, либо из центральной, перепрыгнув через уже пройденную соседнюю. В обоих случаях, снова пойти в соседнюю клетку мини-слон не сможет. В центральную клетку из угловой мини-слон может пойти также не более одного раза. Таким образом, мини-слон покинет угловые клетки не более двух раз, значит, он посетит не более трёх угловых клеток.
Ответ

12 клеток.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет