Олимпиадная задача по планиметрии для 7–8 классов: доказательство перпендикулярности в треугольнике
Задача
Через точку Y на стороне AB равностороннего треугольника ABC проведена прямая, пересекающая сторону BC в точке Z, а продолжение стороны CA за точку A – в точке X. Известно, что XY = YZ и AY = BZ. Докажите, что прямые XZ и BC перпендикулярны.
Решение
Решение 1: Отметим на стороне AC точку T так, что AT = AY, тогда TC = CZ (рис. слева). Оба треугольника ATY и CTZ – равносторонние. Следовательно, ∠YTZ = 60°, то есть TY – биссектриса треугольника XTZ. Но по условию TY – медиана, поэтому треугольник XTZ – равнобедренный, а TY – его высота. Значит, ∠TZY = 30╟, а ∠CZX = 60° + 30° = 90°.
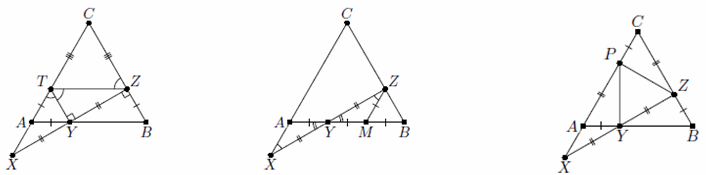
Решение 2: Через точку Z проведём прямую, параллельную стороне AC, которая пересечет сторону AB в точке M (рис. в центре). Ясно, что треугольник BZM – равносторонний. Значит, MZ = BM = BZ = AY.
Кроме того, ∠YZM = ∠YXA, поэтому треугольники MYZ и AYX равны (по стороне и двум прилежащим углам). Следовательно, AX = MZ = AY = MY.
Итак, медиана ZM треугольника BZY равна половине его стороны BY, поэтому этот треугольник прямоугольный.
Решение 3: Отметим на стороне AC точку P так, что CP = AY = BZ (рис. справа).
Тогда CZ = AP = BY. Треугольники CZP, APY и BYZ равны (по двум сторонам и углу между ними), значит, треугольник ZPY – равносторонний. В треугольнике XPZ медиана PY равна половине стороны XZ, поэтому ∠XPZ = 90°, а ∠CXZ = ∠PXZ = 30°. Следовательно,
∠CZX = 180° – ∠CXZ – ∠C = 90°.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь