Олимпиадная задача о равенстве чисел в таблице 10×10: принцип крайнего, 7-8 класс

Решение 1:   Рассмотрим два произвольных подчёркнутых числа A и B. Из условия следует, что они расположены в разных строках и в разных столбцах. Пусть на пересечении строки, в которой находится число A, и столбца, в котором находится число B, стоит число C, а на пересечении строки, в которой находится число B, и столбца, в котором находится число A, стоит число D (см. рис.).

  По условию  B ≤ C ≤ A ≤ D ≤ B.  Следовательно,  A = B.   Таким образом, любые два подчёркнутых числа равны. Рассмотрим теперь произвольное число таблицы, которое не подчёркнуто. Оно не меньше числа, подчёркнутого в его столбце, и не больше числа, подчёркнутого в его строке, следовательно, оно им равно. Итак, все числа между собой равны.

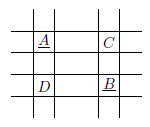
Решение 2:   Пусть в первой строке подчёркнуто число a₁, во второй – a₂, ..., в десятой – a₁₀. Сумма чисел каждой строки не превышает подчёркнутого в этой строке числа, умноженного на 10, причём равенство достигается тогда и только тогда, когда все числа в этой строке равны. Следовательно, сумма всех чисел таблицы  S ≤ 10(a₁ + ... + a₁₀) , и равенство достигается тогда и только тогда, когда в каждой строке все числа одинаковы.

   Проведя аналогичное рассуждение о наименьших числах в столбцах и учитывая, что подчёркнуты те же самые числа, получим, что S ≥ 10(a₁ + ... + a₁₀),  причём равенство достигается тогда и только тогда, когда в каждом столбце все числа одинаковы.

  Таким образом,  S = 10(a₁ + ... + a₁₀),  и в каждой строке, и в каждом столбце стоят одинаковые числа.

Ответ задачи отсутствует