Олимпиадная задача по планиметрии: равнобедренные треугольники в треугольнике ABC
Задача
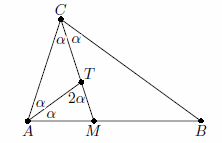
В треугольнике ABC биссектриса угла C пересекает сторону AB в точке M, а биссектриса угла A пересекает отрезок CM в точке T. Оказалось, что отрезки CM и AT разбили треугольник ABC на три равнобедренных треугольника. Найдите углы треугольника ABC.
Решение
Так как сумма углов A и C треугольника ABC меньше, чем 180°, то ∠TAC + ∠TCA < 90°, поэтому угол ATC – тупой (см. рис.).
Ответ
72°, 72° и 36°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет