Олимпиадная задача: Минимум колдобин на маршруте между деревнями (6-8 класс)
Задача
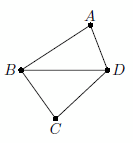
На карте обозначены четыре деревни: A, B, C и D, соединённые тропинками (см. рисунок).
Решение
Существует три возможных маршрута из A в D: 1) A-D; 2) A-B-D; 3) A-B-C-D.
Из того, что на маршруте A-B-D находятся 22 колдобины, следует, что на тропинке B-D их не больше чем 22. Значит, из 45 колдобин маршрута A-D-B не меньше чем 23 колдобины находятся на тропинке A-D. Таким образом, маршрут 2) выгоднее маршрута 1).
Поскольку на маршруте A-B-C есть 10 колдобин, то на тропинке A-B их не больше 10. Значит, из 22 колдобин маршрута A-B-D не менее двенадцати приходится на тропинку B-D. Но на участке B-C-D есть только 10 колдобин, поэтому он выгоднее чем B-D. Итак, маршрут 3) выгоднее маршрута 2).
Ответ
По маршруту A-B-C-D.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь