Олимпиадная задача по планиметрии и стереометрии: периметр треугольного сечения тетраэдра
Задача
Длина ребра правильного тетраэдра равна a. Через одну из вершин тетраэдра проведено треугольное сечение.
Докажите, что периметр P этого треугольника удовлетворяет неравенству P > 2a.
Решение
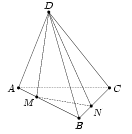
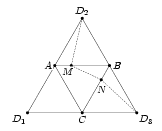
Рассмотрим правильный тетраэдр ABCD. Пусть сечение, описанное в условии, проходит через вершину D и пересекает рёбра AB и BC в точках M и N соответственно (рис. слева). Рассмотрим развертку D2AD1CD3B тетраэдра ABCD на плоскость треугольника ABC (рис. справа).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет