Олимпиадная задача по тригонометрии и планиметрии: угол треугольника ABC
Задача
Про углы треугольника ABC известно, что
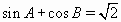 и
и
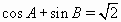 . Найдите величину угла C.
. Найдите величину угла C.
Решение
Первый способ. Возведём оба равенства в квадрат и сложим. Получим 4 = 2 + 2 (sin A cos B + cos A sin B) = 2 + 2 sin (A + B). Следовательно,
sin (A + B) = 1, то есть A + B = 90°.Второй способ. Сложив исходные равенства, получим sin (A + 45°) + sin (B + 45°) = 2, откуда sin (A + 45°) = sin (B + 45°) = 1.
Следовательно, A = B = 45°. Значит, C = 90°.Третий способ. Перемножив исходные равенства, получим sin 2A + sin 2B + 2 cos (A – B) = 4, откуда sin 2A = sin 2B = cos (A – B) = 1, то есть
A = B = 45°.
Ответ
90°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет