Олимпиадная задача по планиметрии: биссектриса, вписанная окружность и треугольник ABC
Задача
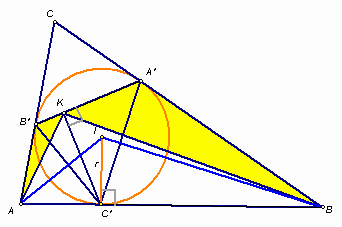
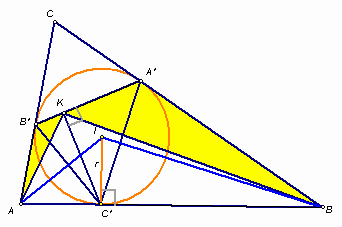
Вписанная окружность треугольника ABC касается его сторон ВС, АС и АВ в точках A', B' и C' соответственно. Точка K – проекция точки C' на прямую A'B'. Докажите, что KC' – биссектриса угла AKB.
Решение
Прежде всего отметим, что точка K лежит между точками A' и B', так как треугольник A'B'C' – остроугольный. Действительно, нетрудно проверить, что, например, угол A'B'C' равен 90° – ½ ∠A.
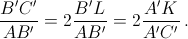Аналогично 
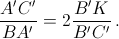Перемножая эти равенства, получим
откуда следует подобие треугольниковAB'KиBA'K(углыAB'KиBA'Kравны как смежные к углам равнобедренного треугольникаA'CB'). Значит, углыAKB'иBKA'равны, что эквивалентно утверждению задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет