Олимпиадная задача по планиметрии для 9–11 классов. Докажите свойство высот треугольника
Задача
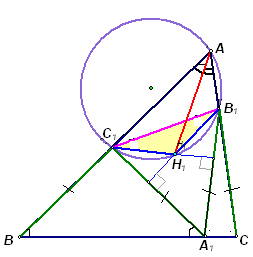
На сторонах АВ, ВС и СА треугольника АВС отмечены точки С1, А1 и В1 соответственно так, что ВС1 = С1А1 = А1В1 = В1С.
Докажите, что точка пересечения высот треугольника С1А1В1 лежит на биссектрисе угла А.
Решение
Так как треугольники ВС1А1 и А1В1С – равнобедренные, то ∠С1А1В = ∠В, ∠В1А1С = ∠С (см. рис.). Тогда ∠С1А1В1 = 180° – (∠ В + ∠ С) = ∠ A.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет