Назад

Олимпиадная задача по планиметрии: площади треугольников внутри параллелограмма

Задача 216434 • Сложность: 1 • 9-11 класс
Задача

Внутри параллелограмма ABCD выбрана произвольная точка Р и проведены отрезки РА, РВ, РС и PD. Площади трёх из образовавшихся треугольников равны 1, 2 и 3 (в каком-то порядке). Какие значения может принимать площадь четвёртого треугольника?

Авторы:
Фольклор
Разделы:
Планиметрия
Источники:
Московская математическая регата Олимпиады и турниры 2011/12 11 класс
Количество версий:
4
Решение

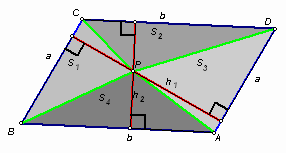
  Введём обозначения так, как показано на рисунке. Заметим, что   S1 + S3 = S2 + S4.   Действительно,  S1 + S3 = ½ ah1 = ½ SABCD = ½ bh2 = S2 + S4.

  Поэтому площадь четвёртого треугольника равна  1 + 3 – 2 = 2  или  2 + 3 – 1 = 4,  или  1 + 2 – 3 = 0.  Последний случай невозможен.

  Для квадрата нетрудно построить примеры, где площади образовавшихся треугольников относятся как  1 : 2 : 3 : 2  или  1 : 2 : 4 : 3.

Ответ

2 или 4.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет