Олимпиадная задача по теории чисел: разрезание сыра на равные части — Шаповалов А. В.
Задача
а) Есть кусок сыра. Разрешается выбрать любое положительное (возможно, нецелое) число a ≠ 1, и разрезать этот кусок в отношении 1 : a по весу, затем разрезать в том же отношении любой из имеющихся кусков, и т. д. Можно ли действовать так, что после конечного числа разрезаний весь сыр удастся разложить на две кучки равного веса?
б) Тот же вопрос, но выбирается положительное рациональное a ≠ 1.
Решение
а) Разрезание в отношении 1 : a равносильно отрезанию доли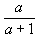 
. Выберем такое a, что 
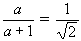, и разрежем во второй раз наибольший из кусков. Тогда вес самого большого из полученных кусков равен половине веса всего сыра. б) Допустим противное: после нескольких разрезаний удалось разбить все куски на две равные кучки. Без ограничения общности можно считать, что мы резали на каждом шагу все имеющиеся куски. После k шагов получились куски, чьи веса относятся как 1 : a : a² : ... : ak, причём 1 и ak соответствует ровно по одному куску. Подставив вместо a несократимую дробь m/n и умножив все веса на подходящую константу, получим целые веса nk, mnk–1, ..., mk. m и n взаимно просты, поэтому вес одной кучки кратен m, а другой, где есть кусок веса nk, не кратен. Противоречие.
Ответ
а) Можно. б) Нельзя.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь