Олимпиадная задача по делимости произведений с многочленами и индукцией (10-11 класс)

Решение 1:   Пусть 1_k – число из k единиц, тогда  [m]! = 1_m·[m–1]!,  1_m+n = 10^m·1_n + 1_m.  Обозначим 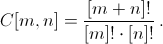    Положим  [0]! = 1,  тогда C[0, n] и C[m, 0] определены и равны 1. Докажем индукцией по  m + n,  что число  C[m, n]  целое. База и случай  m = 0  или  n = 0  очевидны.

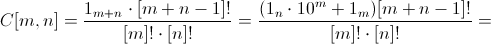
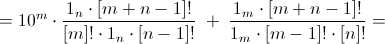
  Шаг индукции. Пусть  m, n ≥ 1  и для меньших значений  m + n  все доказано. Тогда число   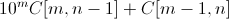      тоже целое.

Решение 2:   Пусть q – число, взаимно простое с 10,  k(q) = min {k| 1_k   кратно q}. Тогда 1_k кратно q тогда и только тогда, когда k кратно k(q). Поэтому из множителей вида 1_k, входящих в [n]!, на q делятся ровно 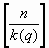 .   Из этого следует, что простое число  p ≠ 2, 5  входит в разложение [n]! на простые множители в степени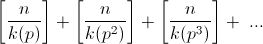  

  В силу неравенства 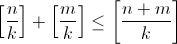    каждое простое число входит в разложение [n+m]! не в меньшей степени, чем в разложение [n]!·[m]!.

Решение 3: Для знатоков. Рассмотрим многочлены   P_k(x) = x^k–1 + x^k–2 + ... + x + 1,   Q_n(x) = P₂(x)... P_n(x)   (над полем комплексных чисел). Достаточно доказать, что Q_m+n(x) делится на Q_n(x)Q_m(x). Действительно, Q_n(x)Q_m(x) – приведённый многочлен, частное – многочлен с целыми коэффициентами. Подставив  x = 10,  получаем утверждение задачи.   Первый способ. Корнями многочлена P_k(x) являются все (кроме единицы) корни k-й степени из единицы. Пусть ε – первообразный корень k-й степени из 1. Тогда он является корнем l-й степени тогда и только тогда, когда l кратно k. Поэтому множитель  x – ε  входит в разложение Q_m+n(x) на линейные множители в степени  [^m+n/_k],  а в Q_n(x)Q_m(x) – в степени 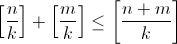   .   Следовательно, Q_m+n(x) делится на Q_n(x)Q_m(x).   Второй способ. Достаточно доказать, что P_n+m(x)P_n+m–1(x)...P_m+1(x) делится на Q_n(x). Это эквивалентно тому, что многочлен

U(x) = (x^n+m – 1)(x^n+m–1 – 1)...(x^m+1 – 1)   делится на  V(x) = (xⁿ – 1)(x^n–1 – 1)...(x – 1).

  Поделим с остатком:  U(x) = W(x)V(x) + R(x),  где W(x) и R(x) – многочлены с целыми коэффициентами, и предположим, что  R(x) ≠ 0.  Поскольку

deg R(x) < degV(x),  при больших натуральных k выполнено неравенство  0 < |R(k)| < |V(k)|,  то есть число U(k) не кратно V(k).

  Но, как известно, для любого простого числа p количество n-мерных подпространств в 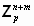равно 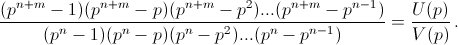    Противоречие.

Ответ задачи отсутствует