Олимпиадная задача: сравнение чисел на неравенствах и делимости (Горяшин Д. В.)
Задача
Сравните числа 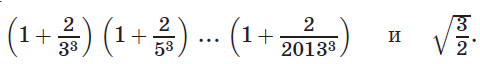
Решение
Обозначим первое число через A, а второе через B и докажем, что A < B. Первый способ.
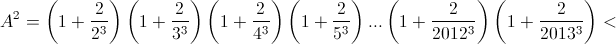
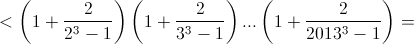

 (последняя оценка следует из результата задачи 161446 в). С другой стороны, B6 = (3/2)³ > 3 > e, поэтому ln B > ⅙.
(последняя оценка следует из результата задачи 161446 в). С другой стороны, B6 = (3/2)³ > 3 > e, поэтому ln B > ⅙.
Ответ
Первое число меньше.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет