Олимпиадная задача Лопатникова: Раскраска клетчатой плоскости — комбинаторная геометрия
Задача
Можно ли так раскрасить все клетки бесконечной клетчатой плоскости в белый и чёрный цвета, чтобы каждая вертикальная прямая и каждая горизонтальная прямая пересекали конечное число белых клеток, а каждая наклонная прямая конечное число чёрных?
Решение
Введём такую систему координат Oxy, чтобы вертикальные и горизонтальные и линии сетки имели уравнения x = n и y = m (n и m – целые). Раскрасим в чёрный цвет те и только те клетки, все точки которых удовлетворяют одному из неравенств |y| ≥ x² или |x| ≥ y² (см. рис.), остальные клетки покрасим в белый цвет.
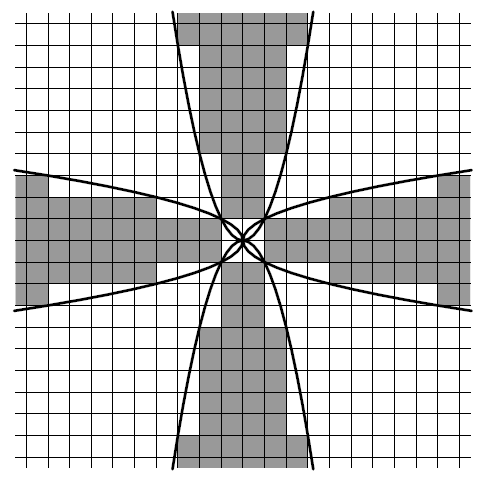
Ответ
Можно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет