Олимпиадная задача по планиметрии: сколько квадратов уместит Петя вокруг круга
Задача
На столе лежит картонный круг радиуса 5 см. Петя, пока возможно, прикладывает к кругу снаружи картонные квадраты со стороной 5 см так, чтобы выполнялись условия:
1) у каждого квадрата одна вершина лежит на границе круга;
2) квадраты не пересекаются;
3) каждый следующий квадрат касается предыдущего вершиной к вершине.
Определите, сколько квадратов может выложить Петя, и докажите, что последний и первый квадрат тоже коснутся вершинами.
Решение
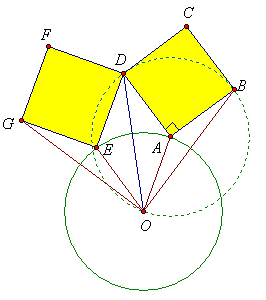
Если вершина A квадрата ABCD лежит на окружности с центром O, то точки B, D и O лежат на окружности радиуса 5 см с центром A. Вписанный угол BOD равен 45°, то есть каждый выложенный квадрат виден из центра под углом 45°. Границы соседних углов совпадают, поэтому всего Петя сможет выложить 8 квадратов.
Пусть EDFG – еще один выложенный квадрат (E лежит на окружности). OADE – ромб, поэтому ∠OAD = ∠OED. Отсюда
∠OAB = 360° – 90° – ∠OAD = 360° – 90° – ∠OED = ∠OEG.
Треугольники OAB и OEG равны по двум сторонам и углу, значит, OB = OG. Итак, вершины квадратов, противоположные общей вершине, равноудалены от O. Таким образом, одна из вершин первого квадрата и одна из вершин восьмого лежат на одном и том же луче, выходящем из O, на одинаковом расстоянии от O. Поэтому они совпадают.
Ответ
8 квадратов.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь