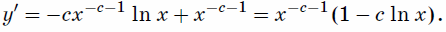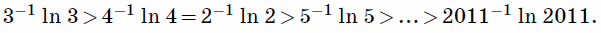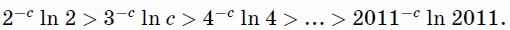Пусть a1, a2, ..., a2011
— искомая расстановка чисел. Нетрудно видеть, что
тогда должно быть выполнено равенство a2011 = 1, так как иначе выражение из условия
задачи можно было бы увеличить, поменяв между собой местами числа ak = 1
(k ≠ 2011) и a2011 .Сравним два числа  и
и 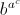 , где
a, b и c — некоторые натуральные числа, причём
a ≠ b, a ≥ 2 и
b ≥ 2. Так как функция y = ln x монотонно возрастает при всех
x > 0, то разность
, где
a, b и c — некоторые натуральные числа, причём
a ≠ b, a ≥ 2 и
b ≥ 2. Так как функция y = ln x монотонно возрастает при всех
x > 0, то разность  –
–
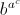 имеет тот
же знак, что и разность
имеет тот
же знак, что и разность
Найдём промежутки монотонности функции
y=
x – cln
x. Имеем
Так как
y'
>0 при 0
< x < e1/cи
y'
<0
при
x > e1/c, то функция
y=
x – cln
xвозрастает на
промежутке 0
< x < e1/cи убывает на промежутке
x > e1/c.При
c = 1, учитывая неравенство 3
> e, отсюда получаем
Значит,
a – 1ln
a > b – 1ln
b, если 3 ≤
a < b.
Следовательно,
ab1> ba1при 3 ≤
a < b. При
c≥ 2 имеем
1
< e1/c <2. Поэтому при таких значениях
cполучаем, что
Тогда
a – c ln
a > b – cln
bи
abc> ba
cпри 2 ≤
a < b.Докажем по индукции, что для искомой расстановки чисел и всех
n = 1, 2, ...,
2010 имеет место
равенство
a2011 – n = 2012 –
n. Пусть сначала
n = 1.
Если 2011 =
ak, где
k ≤ 2009, то 2 ≤
ak+1
< ak и,
по доказанному выше,
akak+1
c < a
k+1akc при всех натуральных
c. Поэтому выражение из условия
задачи можно увеличить, поменяв между собой местами числа
ak = 2011 и
ak+1. Полученное
противоречие означает, что
a2010 = 2011. Аналогичными рассуждениями доказываются и следующие
шаги индукции: считая уже доказанным равенство
a2011 – n = 2012 –
n при некотором натуральном
n ≤ 2007 и предполагая, что
a2011 – (n + 1) ≠ 2012 –
(
n + 1), приходим к противоречию, так как
по доказанному выше
akak + 1c
< a
k+1akc при 2012 – (
n + 1) =
ak, где
k ≤ 2011 – (
n + 2).
Значит,
a3 = 4,
a4 = 5, ...,
a2010 = 2011
и
a2011 = 1. Для доказательства того, что
a1 = 2 и
a2 = 3, заметим, что при
c = 4
5...2011
> 2 имеет место неравенство 2
3c
> 3
2c. Следовательно,
выражение из условия задачи будет наибольшим при
a1 = 2,
a2 = 3, ...,
a2010 = 2011 и
a2011 = 1.
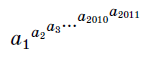
 и
и 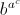 , где
a, b и c — некоторые натуральные числа, причём
a ≠ b, a ≥ 2 и
b ≥ 2. Так как функция y = ln x монотонно возрастает при всех
x > 0, то разность
, где
a, b и c — некоторые натуральные числа, причём
a ≠ b, a ≥ 2 и
b ≥ 2. Так как функция y = ln x монотонно возрастает при всех
x > 0, то разность  –
–
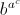 имеет тот
же знак, что и разность
имеет тот
же знак, что и разность