Олимпиадная задача по планиметрии для 9–11 классов: точка O внутри треугольника
Задача
Внутри треугольника ABC взята такая точка O, что ∠ABO = ∠CAO, ∠BAO = ∠BCO, ∠BOC = 90°. Найдите отношение AC : OC.
Решение
Построим точку D, симметричную точке C относительно прямой BO (см. рис.). Тогда ∠BDO = ∠BCO = ∠BAO. Значит, точка D лежит на описанной окружности треугольника ABO, и ∠ADO = ∠ABO = ∠CAO. Значит, треугольник DAC подобен треугольнику AOC. Следовательно, DC : AC = AC : OC, или 2OC : AC = AC : OC, откуда 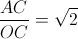 .
.
Ответ
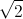 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет