Олимпиадная задача по стереометрии: максимальный радиус круга в проекции тетраэдра
Задача
Рассматриваются ортогональные проекции данного правильного тетраэдра с единичным ребром на всевозможные плоскости. Какое наибольшее значение может принимать радиус круга, содержащегося в такой проекции?
Решение
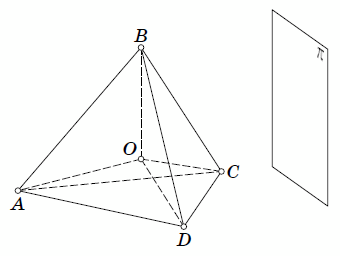
Пусть A, B, C и D — вершины этого тетраэдра,
O — его центр (см. рис. а).
Спроецируем тетраэдр ортогонально на некоторую плоскость π. Обозначим через A',
B', C', D' и O'
ортогональные проекции точек A, B, C, D и O на плоскость π соответственно.
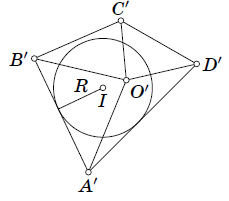
Если плоскость π
параллельна рёбрам AB и CD, то проекция представляет собой квадрат с диагональю длины 1 (см.
рис. б). В этот квадрат можно вписать круг радиуса 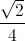 .Приведём два способа дальнейшего решения задачи.
.Приведём два способа дальнейшего решения задачи.
Первый способ. Предположим, что найдётся такая плоскость π, что ортогональная проекция
правильного тетраэдра ABCD с ребром длины 1 на эту плоскость содержит некоторый круг с
центром в точке I и радиусом R > 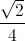 .
Проекция тетраэдра представляет собой либо
четырёхугольник с вершинами в точках A', B', C', D' (см. рис. в),
либо треугольник с вершинами в
трёх из этих точек (см. рис. г). Рассмотрим треугольники O'A'B',
O'A'C', O'B'C', O'A'D',
O'B'D' и
O'C'D'. По крайней мере один из этих треугольников имеет сторону,
являющуюся также стороной в
этой проекции, и содержит точку I. Пусть для определённости это треугольник O'A'B'.
Тогда расстояние от ребра AB до прямой l, проходящей через точку I перпендикулярно
к плоскости π, не меньше R и больше
.
Проекция тетраэдра представляет собой либо
четырёхугольник с вершинами в точках A', B', C', D' (см. рис. в),
либо треугольник с вершинами в
трёх из этих точек (см. рис. г). Рассмотрим треугольники O'A'B',
O'A'C', O'B'C', O'A'D',
O'B'D' и
O'C'D'. По крайней мере один из этих треугольников имеет сторону,
являющуюся также стороной в
этой проекции, и содержит точку I. Пусть для определённости это треугольник O'A'B'.
Тогда расстояние от ребра AB до прямой l, проходящей через точку I перпендикулярно
к плоскости π, не меньше R и больше 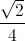 .
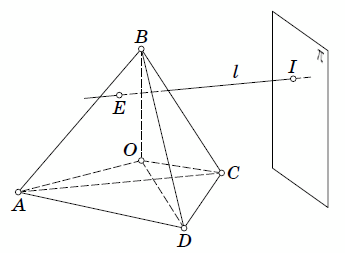
С другой стороны, эта прямая пересекает
треугольник OAB в некоторой точке E (см. рис. д). Расстояние же от точки E до ребра AB не
превосходит расстояния от точки O до этого ребра, то есть не больше
.
С другой стороны, эта прямая пересекает
треугольник OAB в некоторой точке E (см. рис. д). Расстояние же от точки E до ребра AB не
превосходит расстояния от точки O до этого ребра, то есть не больше
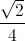 .
Полученное
противоречие показывает, что такой плоскости π и такой ортогональной проекции не
существует.
.
Полученное
противоречие показывает, что такой плоскости π и такой ортогональной проекции не
существует.
 |
 |
 |
| Рис. а | Рис. б | Рис. в |
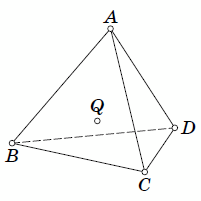
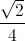 .Проекция тетраэдра — это или треугольник, или четырёхугольник. Если проекция —
треугольник, то это проекция грани тетраэдра. Пусть, для определённости, это грань ABC (см.
рис. е). В эту грань тетраэдра впишем окружность с центром в точке Q и
радиусом
.Проекция тетраэдра — это или треугольник, или четырёхугольник. Если проекция —
треугольник, то это проекция грани тетраэдра. Пусть, для определённости, это грань ABC (см.
рис. е). В эту грань тетраэдра впишем окружность с центром в точке Q и
радиусом 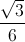 (
(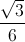 <
<
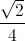 ).
Пусть Q' — проекция Q, тогда круг с центром в точке Q'
и радиусом
).
Пусть Q' — проекция Q, тогда круг с центром в точке Q'
и радиусом 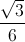 содержит середины
сторон проекции A'B'C' и либо вписан в треугольник-проекцию, либо выходит за его
пределы. В последнем случае проведём касательные к этому кругу, параллельные сторонам
треугольника-проекции (см. рис. ж). Получим описанный около этого круга треугольник A''B''C'',
который содержит треугольник A'B'C' внутри себя. Значит, если в проекции можно расположить
круг радиуса большего, чем
содержит середины
сторон проекции A'B'C' и либо вписан в треугольник-проекцию, либо выходит за его
пределы. В последнем случае проведём касательные к этому кругу, параллельные сторонам
треугольника-проекции (см. рис. ж). Получим описанный около этого круга треугольник A''B''C'',
который содержит треугольник A'B'C' внутри себя. Значит, если в проекции можно расположить
круг радиуса большего, чем 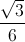 ,
то этот круг расположится и в треугольнике A''B''C'', что
невозможно.
,
то этот круг расположится и в треугольнике A''B''C'', что
невозможно.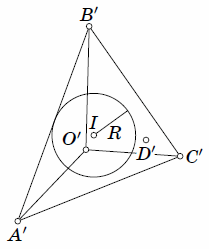 |
 |
 |
| Рис. г | Рис. д | Рис. е |
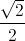 .
Рассмотрим круг с центром в точке P и радиусом
.
Рассмотрим круг с центром в точке P и радиусом 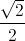 .
Этот круг содержит указанный параллелограмм и либо вписан в четырёхугольник-проекцию, либо выходит за его
пределы. В последнем случае проведём касательные к этому кругу, параллельные сторонам
четырёхугольника-проекции. Получим описанный около этого круга четырёхугольник A''B''C''D'',
который содержит четырёхугольник A'B'C'D'
внутри себя. Значит, если в A'B'C'D' можно
расположить круг радиуса большего, чем
.
Этот круг содержит указанный параллелограмм и либо вписан в четырёхугольник-проекцию, либо выходит за его
пределы. В последнем случае проведём касательные к этому кругу, параллельные сторонам
четырёхугольника-проекции. Получим описанный около этого круга четырёхугольник A''B''C''D'',
который содержит четырёхугольник A'B'C'D'
внутри себя. Значит, если в A'B'C'D' можно
расположить круг радиуса большего, чем 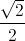 ,
то этот круг разместится и в четырёхугольнике
A'' B'' C'' D'', что невозможно.
,
то этот круг разместится и в четырёхугольнике
A'' B'' C'' D'', что невозможно.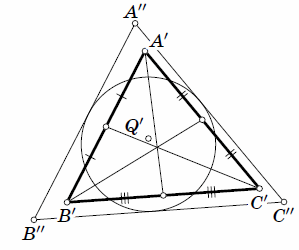 |
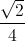 |
| Рис. ж | Рис. з |
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь