Олимпиадная задача: сравнение наименьших положительных корней многочленов для 10-11 класса

Решение 1:Пусть  x₁ > 0  – корень уравнения  x²⁰¹¹ + 2011x – 1,  а  x₂ > 0  – корень уравнения  x²⁰¹¹ – 2011x + 1.  Тогда 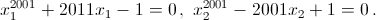    Складывая эти равенства почленно, получаем     Значит, 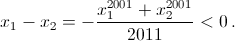    Таким образом,  x₁ < x₂.

Решение 2:Функция x²⁰¹¹ принимает только положительные, а функция  2011x – 1  – только отрицательные значения на интервале  (0, ¹/₂₀₁₁).  Значит, уравнение  x²⁰¹¹ = 2011x – 1  и многочлен  x²⁰¹¹ – 2011x + 1  не имеют корней на этом интервале. Многочлен  x²⁰¹¹ + 2011x – 1  принимает в концах отрезка

[0, ¹/₂₀₁₁]  значения разных знаков и, следовательно, имеет корень на интервале (0, ¹/₂₀₁₁).

У первого многочлена наименьший положительный корень меньше.