Олимпиадная задача по математике: примеры и конструкции для 8-10 классов
Задача
На доске написаны три натуральных числа, не превосходящих 40. За один ход можно увеличить любое из написанных чисел на число процентов, равное одному из двух оставшихся чисел, если в результате получится целое число. Существуют ли такие исходные числа, что за несколько ходов одно из чисел на доске можно сделать больше 2011?
Решение
Приведём два примера возможных изначальных чисел и последовательностей преобразований (разумеется, для полного решения задачи достаточно привести всего один пример).
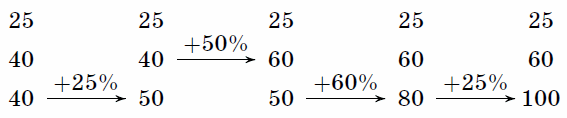 |
| Рис. а |
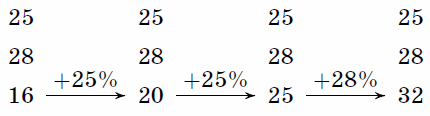 |
| Рис. б |
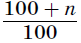 .
Поэтому результат увеличения числа
x на n% будет целым, если и только если произведение x(100 + n) будет делиться на
100.Допустим, что мы будем всё время увеличивать только одно из чисел. При каждом таком
увеличении мы умножаем число на дробь со знаменателем 100; поэтому нам нужно позаботиться о
том, чтобы итоговое число продолжало делиться на достаточно большие степени двойки и пятёрки.
Значит, на достаточно большие степени двойки и пятёрки должны делиться числители дробей, на
которые мы умножаем. Поскольку каждая отдельная дробь (соответствующая значениям n ≤ 40)
целой быть не может, естественно возникает идея "разделения обязанностей": у части дробей
числители будут делиться на большую степень двойки (но на недостаточную — пятёрки), а у части
— наоборот.На большую степень двойки делится, например, число 128 = 27,
а на большую степень пятёрки —
число 125 = 53. Используя дроби
.
Поэтому результат увеличения числа
x на n% будет целым, если и только если произведение x(100 + n) будет делиться на
100.Допустим, что мы будем всё время увеличивать только одно из чисел. При каждом таком
увеличении мы умножаем число на дробь со знаменателем 100; поэтому нам нужно позаботиться о
том, чтобы итоговое число продолжало делиться на достаточно большие степени двойки и пятёрки.
Значит, на достаточно большие степени двойки и пятёрки должны делиться числители дробей, на
которые мы умножаем. Поскольку каждая отдельная дробь (соответствующая значениям n ≤ 40)
целой быть не может, естественно возникает идея "разделения обязанностей": у части дробей
числители будут делиться на большую степень двойки (но на недостаточную — пятёрки), а у части
— наоборот.На большую степень двойки делится, например, число 128 = 27,
а на большую степень пятёрки —
число 125 = 53. Используя дроби 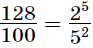 и
и
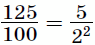 , уже несложно подобрать последовательность
операций, приводящую к умножению на целое число:
, уже несложно подобрать последовательность
операций, приводящую к умножению на целое число:
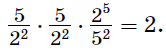
Осталось выбрать начальное значение третьего числа таким, чтобы первые два шага не привели к дробным числам, и мы можем повторять увеличения на 25%, 25% и 28% циклически.
Ответ
да, существуют.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет