Олимпиадная задача по планиметрии для 8–10 классов: перпендикулярность AI и CD

Задача

В прямоугольном треугольнике ABC с прямым углом C угол A равен 30°, точка I – центр вписанной окружности ABC, D – точка пересечения отрезка BI с этой окружностью. Докажите, что отрезки AI и CD перпендикулярны.

Решение

Пусть E – точка касания вписанной окружности и стороны BC. Заметим, что CE = IE (см. рис.).

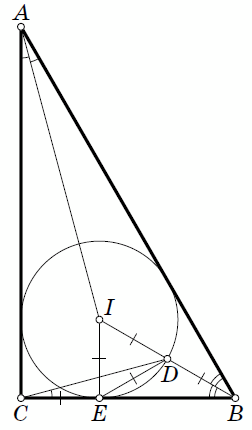
В прямоугольном треугольникеIEBуголIBEравен 30°, значит, ∠EIB= 60°. Следовательно, треугольникIDEравносторонний. По доказанному CE = IE = DE, то есть треугольникCDEравнобедренный. Угол при вершинеEравен ∠CED= 180° – 30° = 150°. Следовательно, ∠DCE= 15°. Осталось заметить, что ∠IAC+ ∠ACD= 15° + (90° – ∠DCE) = 90°, а значит, AI⊥CD.

Ответ

Ответ задачи отсутствует

Олимпиадная задача по планиметрии: перпендикулярность в треугольнике ABC для 8–10 классов

Задача

Решение

Ответ

Подтверждение удаления