Олимпиадная задача по планиметрии о точках на трапеции для 8-9 класса (Волчкевич М. А.)
Задача
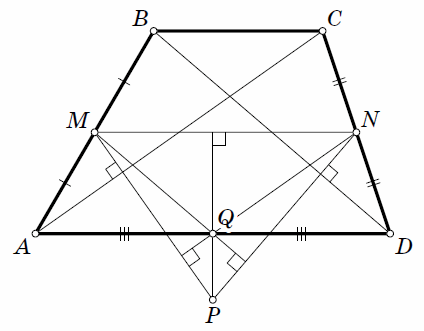
Точки M и N – середины боковых сторон AB и CD трапеции ABCD. Перпендикуляр, опущенный из точки M на диагональ AC, и перпендикуляр, опущенный из точки N на диагональ BD, пересекаются в точке P. Докажите, что PA = PD.
Решение
Обозначим через Q середину стороны AD (см. рис.). Заметим, что MQ || BD, QN || AC как средние линии треугольников ABD и ACD соответственно. Поэтому прямые MP и NP – высоты треугольника MNQ, а P – его ортоцентр. Значит, QP ⊥ MN || AD, то есть QP – серединный перпендикуляр к отрезку AD. Следовательно, PA = PD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет