Олимпиадная задача: Несамопересекающаяся ломаная на квадрате 100×100 в планиметрии
Задача
Каждое звено несамопересекающейся ломаной состоит из нечётного числа сторон клеток квадрата 100×100, соседние звенья перпендикулярны.
Может ли ломаная пройти через все вершины клеток?
Решение
Предположим, что ломаная, обладающая указанными свойствами, существует. Рассмотрим ту из сторон квадрата, которой не принадлежит ни один из концов ломаной. Если такой стороны нет, то есть ломаная идёт из одного угла квадрата в другой, то рассмотрим ту из сторон, вдоль которой направлено первое звено ломаной (см. рис.). Каждый из узлов этой стороны принадлежит некоторому (причём ровно одному) звену ломаной, идущему вдоль стороны квадрата. Действительно: если узел не является концом ломаной, то есть два звена, его содержащие, и одно из них обязано идти вдоль стороны. Если же узел является концом ломаной, то выполнение этого свойства гарантировано выбором стороны.
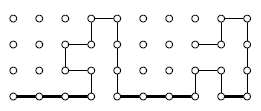
Ответ
Не может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь