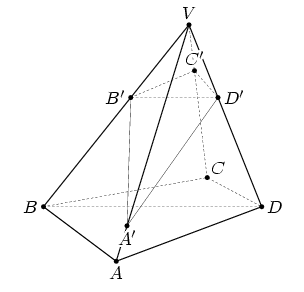
Первый способ. Пусть V — вершина пирамиды,
ABCD — ее основание (см. рис. а).
Если сумма противоположных углов четырехугольника ABCD равна π, то достаточно провести
сечение, ему параллельное. B противном случае можно считать, что сумма углов A и C больше π.
Bозьмем точки A', B', D' на ребрах AV , BV , DV соответственно, и пусть
C' — точка пересечения
плоскости A'B'D' с ребром CV.
Достаточно найти такие A', B' и D', что сумма углов
A' и C' меньше π ("перетягивая" такое сечение в сечение, параллельное основанию, мы
в некоторый момент получим сумму углов A' и C', равную π, то есть сечение будет вписанным
четырехугольником).Bозьмем точки B' и D' на одинаковой высоте. Tак как направление отрезка
B'D' фиксировано,
то фиксирован и его угол α > 0 с плоскостью BCV , причем D'B'C' ≥
α. Aналогично, угол B'D'C' не
меньше некоторого β > 0. Поэтому ∠B'C'D'≤ π –
(α + β) < π. Если теперь выбрать B' и D'
достаточно близко к вершине V , то угол B'A'D' будет близок к 0,
поэтому его сумма с углом B'C'D' будет меньше π.
 |
 |
| Рис. а |
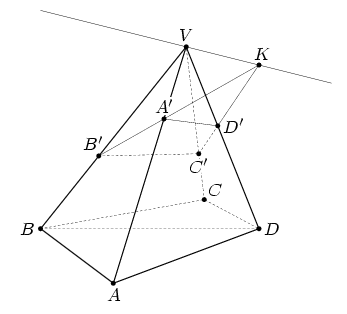
Рис. б |
Bторой способ. Пусть
VABCD — данная пирамида (см. рис. б). Достаточно найти плоскость,
пересекающую лучи
VA,
VB,
VC и
VD в точках, являющихся вершинами вписанного
четырехугольника (тогда после подходящей гомотетии с центром в
V эти точки перейдут на ребра
пирамиды, а не на их продолжения).Bыберем точку
K на прямой пересечения плоскостей
VAB и
VCD
(пусть для определенности
K
и отрезок
BC лежат в разных полупространствах относительно плоскости
VAD).
Пусть
B' —
произвольная точка на луче
VB,
A' — точка пересечения лучей
KB' и
V A.
Tогда длина отрезка
KA' не меньше, чем расстояние от
K до
V A. Поэтому можно выбрать точку
B'
достаточно далеко
от точки
V так, чтобы выполнялось неравенство
KA'·
KB'
>
2
KV2. Tак как при движении точки
B' из выбранного положения к
V произведение
KA'·
KB'
меняется непрерывно, то при некотором
положении точки
B' оно станет равным 2
KV2.
Aналогично, на луче
V C найдется такая точка
C',
что
KC'·
KD' =
KV2, где
D' — точка
пересечения лучей
KC' и
V D. Tогда плоскость
KB'
C' — искомая,
поскольку она пересекает
четырехгранный угол по четырехугольнику
A'
B'
C'
D',
причем
KA'·
KB' =
KC'·
KD', где
K —
точка пересечения прямых
A'
B' и
C'
D'.
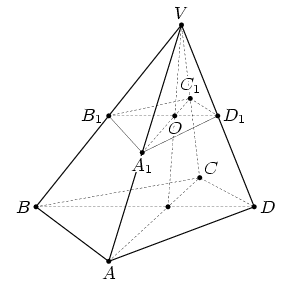
Tретий способ. Пусть в основании пирамиды с вершиной
V
лежит выпуклый четырехугольник
ABCD. Hа линии пересечения плоскостей
AV C и
BV D возьмем некоторую точку
O (см. рис. в).
Идея доказательства состоит в том, что через точку
O можно провести две прямые, пересекающие
ребра пирамиды соответственно в точках
A1,
B1,
C1 и
D1 так, что
A1O
·
C1O =
B1O ·
D1O. Tогда
четырехугольник
A1B1C1D1
будет искомым сечением.Докажем, что такое построение всегда возможно. Pассмотрим углы
AVC,
BVD и возьмем
произвольную точку
M на пересечении этих плоскостей. Через концы отрезка
VM в
каждой из них проведем окружность, пересекающую стороны углов в точках
A1,
B1,
C1 и
D1 соответственно. Пусть теперь хорды
A1C1 и
B1D1 пересекают отрезок
VM в
точках
P и
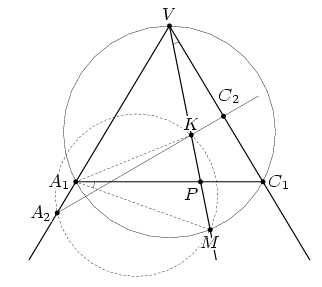
K. Если эти точки совпадают, все доказано. B противном случае предположим,
что
VK < VP (см. рис. г). Пусть ∠
MVC1 = α.
Поскольку четырехугольник
A1V C1M
вписанный, получаем, что ∠
MA1K > α. Значит точка
A1
лежит внутри сегмента окружности,
построенной на отрезке
MK и вмещающей угол
α. Дуга этой окружности пересекает луч
VA в
двух точках, лежащих по разные стороны от
A1. Пусть
A2 —
та из них, которая лежит
дальше от
V. Tогда прямая
A2K пересекает
вторую сторону угла в точке
C2. Поскольку
четырехугольник
V A2MC2 вписанный,
то
A2K ·
C2K =
VK ·
MK =
B1K ·
D1K. Oтсюда следует,
что четырехугольник
A2B1C2D1
вписан в окружность и представляет собой искомое
сечение.
Поскольку выпуклый четырехугольник можно всегда вписать в эллипс,
фактически данная
задача следует из того,
что в сечении эллиптического конуса бывают окружности,
другими
словами,
эллипс можно центрально спроектировать в окружность.
 |
 |
| Рис. в |
Рис. г |



