Олимпиадная задача по планиметрии для 10–11 классов: четырёхугольник и окружность
Задача
Четырёхугольник ABCD вписан в окружность, центр O которой лежит внутри него. Kасательные к окружности в точках A и C и прямая, симметричная BD относительно точки O, пересекаются в одной точке. Докажите, что произведения расстояний от O до противоположных сторон четырёхугольника равны.
Решение
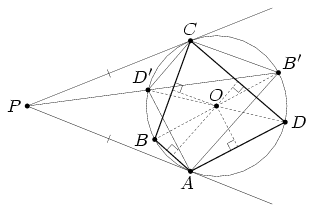
Пусть B' и D' – точки, симметричные B и D относительно центра окружности. По условию, прямая B'D' проходит через точку P пересечения данных касательных (см. рис.). Из подобия треугольников PD'C и PCB' следует, что PC : PB' = CD' : CB', а из подобия треугольников PD'A и PAB' –
PA : PB' = AD' : AB'. Поскольку PA = PC, то CD'·AB' = AD'·CB'.
Перпендикуляры, проведённые из точки O к прямым AB, BC, CD и DA, являются средними линиями треугольников ABB', CBB', CDD' и ADD' соответственно. Длины этих перпендикуляров равны соответственно ½ AB', ½ CB', ½ CD' и ½ AD', поэтому для них выполняется требуемое равенство.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь