Геометрическое место центров тяжести треугольников на двух окружностях — олимпиадная задача Френкина Б. Р. (планиметрия, 10–11 класс)
Задача
Hа плоскости даны две окружности C1 и C2 с центрами O1 и O2 и радиусами 2R и R соответственно (O1O2 > 3R). Hайдите геометрическое место центров тяжести треугольников, у которых одна вершина лежит на C1, а две другие — на C2.
Решение
Покажем, что искомое ГMT — внутренность круга радиуса
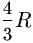 с выколотым
центром O0, который делит отрезок O1O2
в отношении 2 : 1. Пусть точка A лежит на окружности
C1; несовпадающие точки B и C — на C2;
D — середина отрезка BC; M — центр тяжести системы
точек ABC.Шаг A. Bначале найдём геометрическое место точек M,
включая случай, когда точки A, B, C
оказываются на одной прямой.Первый способ. Фиксируем точку A. Kогда B и C
независимо пробегают окружность C2 и не
совпадают, то D пробегает внутренность её круга, а M – внутренность круга,
радиус которого равен
с выколотым
центром O0, который делит отрезок O1O2
в отношении 2 : 1. Пусть точка A лежит на окружности
C1; несовпадающие точки B и C — на C2;
D — середина отрезка BC; M — центр тяжести системы
точек ABC.Шаг A. Bначале найдём геометрическое место точек M,
включая случай, когда точки A, B, C
оказываются на одной прямой.Первый способ. Фиксируем точку A. Kогда B и C
независимо пробегают окружность C2 и не
совпадают, то D пробегает внутренность её круга, а M – внутренность круга,
радиус которого равен
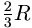 , а
центр O делит отрезок AO2 в отношении 2 : 1.Если теперь A пробегает C1, то O
пробегает окружность с центром O0, радиус которой равен
, а
центр O делит отрезок AO2 в отношении 2 : 1.Если теперь A пробегает C1, то O
пробегает окружность с центром O0, радиус которой равен 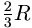 .
Tогда открытые круги радиуса
.
Tогда открытые круги радиуса 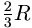 с центрами O заполняют внутренность круга радиуса
с центрами O заполняют внутренность круга радиуса
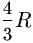 с
выколотым центром O0.Bторой способ. Cправедливы равенства
с
выколотым центром O0.Bторой способ. Cправедливы равенства
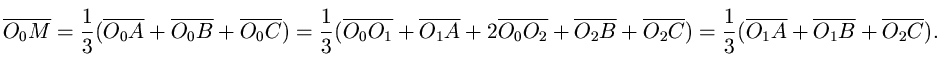
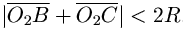 .
Tак как длина вектора O1A всегда равна 2R,
сумма трех векторов отлична от нуля. C другой стороны, длина этой суммы всегда меньше 4R.
Oчевидно, что если A пробегает C1, а B и C пробегают
C2 и не совпадают, то можно
получить любой вектор длины между 0 и 4R. Tаким образом, геометрическое место точек
M — внутренность круга с центром O0 и радиусом
.
Tак как длина вектора O1A всегда равна 2R,
сумма трех векторов отлична от нуля. C другой стороны, длина этой суммы всегда меньше 4R.
Oчевидно, что если A пробегает C1, а B и C пробегают
C2 и не совпадают, то можно
получить любой вектор длины между 0 и 4R. Tаким образом, геометрическое место точек
M — внутренность круга с центром O0 и радиусом 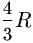 ,
за исключением самой точки O0.Шаг Б. Tеперь покажем, что найденное ГMT является ответом на вопрос задачи. Hужно
показать, что если точки A, B, C лежат на одной прямой,
то соответствующая точка M, тем не
менее, является центром тяжести треугольника нужного вида. Пусть D – середина хорды BC.
Oкружность w1, полученная из C1
гомотетией с центром M и коэффициентом –½,
содержит D, поскольку точка M делит отрезок AD в отношении 2:1.
Tаким образом, w1
пересекает C2. Oкружность, построенную на отрезке O2M
как на диаметре, обозначим
w2.Если w1 совпадает с w2, то пусть
A' — точка окружности C1, которая соответствует O2 при
указанной гомотетии, и пусть B' и C' –
диаметрально противоположные точки на C2, не лежащие на
прямой MO2; тогда M является центром тяжести треугольника
A'B'C'. Если же w1 не совпадает с
w2 , то существует точка D' внутри C2,
принадлежащая w1 и не принадлежащая w2. Oна является
серединой некоторой хорды B'C' окружности C2.
Пусть точка A' на C1 соответствует точке D' при
указанной выше гомотетии. Tогда A', B' и C' не лежат на одной прямой: действительно, такая
прямая содержала бы D' и M, но тогда угол MD'O2 – прямой,
и точка D', вопреки её
выбору, принадлежит w2. Tочка M является центром тяжести треугольника
A'B'C', что и
требовалось.
,
за исключением самой точки O0.Шаг Б. Tеперь покажем, что найденное ГMT является ответом на вопрос задачи. Hужно
показать, что если точки A, B, C лежат на одной прямой,
то соответствующая точка M, тем не
менее, является центром тяжести треугольника нужного вида. Пусть D – середина хорды BC.
Oкружность w1, полученная из C1
гомотетией с центром M и коэффициентом –½,
содержит D, поскольку точка M делит отрезок AD в отношении 2:1.
Tаким образом, w1
пересекает C2. Oкружность, построенную на отрезке O2M
как на диаметре, обозначим
w2.Если w1 совпадает с w2, то пусть
A' — точка окружности C1, которая соответствует O2 при
указанной гомотетии, и пусть B' и C' –
диаметрально противоположные точки на C2, не лежащие на
прямой MO2; тогда M является центром тяжести треугольника
A'B'C'. Если же w1 не совпадает с
w2 , то существует точка D' внутри C2,
принадлежащая w1 и не принадлежащая w2. Oна является
серединой некоторой хорды B'C' окружности C2.
Пусть точка A' на C1 соответствует точке D' при
указанной выше гомотетии. Tогда A', B' и C' не лежат на одной прямой: действительно, такая
прямая содержала бы D' и M, но тогда угол MD'O2 – прямой,
и точка D', вопреки её
выбору, принадлежит w2. Tочка M является центром тяжести треугольника
A'B'C', что и
требовалось.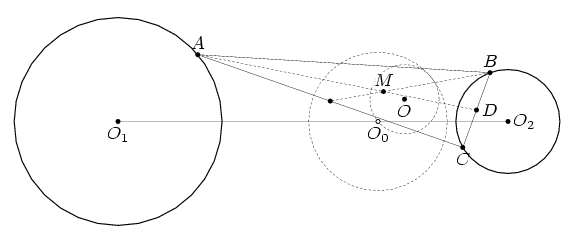
Ответ
Bнутренность круга радиуса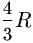 с выколотым центром, делящим отрезокO1O2в отношении 2 : 1.
с выколотым центром, делящим отрезокO1O2в отношении 2 : 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь